The Lorentz Transformation
In the previous section we saw that a combination of a scalar and a vector, a paravector, \(\v{A} = a_0 + \v{a}\), has an amplitude-squared with the same metric as that of spacetime and yet can be rotated like a normal vector such that the scalar part is unchanged, while the vector part rotates in space, as \(\v{\c{R}}\v{A}\v{R}\), where the rotor \(\v{R}\) is itself comprised of a scalar and a bivector, \(\v{R} = e^{-\v{xy}\frac{\theta}{2}}\).
We also saw that we can define a normalised paravector as \(\v{B} = e^{-\v{b}\frac{\phi}{2}}\), so that \(\v{B}\c{\v{B}} = 1\). In this section we will consider rotating the paravector \(\v{A}\) by a normalized paravector and see that the result, \(\v{B}\v{A}\v{B}\), is equivalent to the standard Lorentz transformation.
A hyperbolic rotation
Similar to the spatial rotation, we can see that \(\v{A'} = \v{B}\v{A}\v{B}\) is some type of rotation of \(\v{A}\), as even though we are not using the Clifford conjugation of the rotor for the left-hand multilication, the amplitude squared is still unchanged:
\[ \begin{aligned} \v{\c{A'}A'} &= \c{\v{B}\v{A}\v{B}} \v{B}\v{A}\v{B} \\ &= \c{\v{B}}\c{\v{A}}\c{\v{B}} \v{B}\v{A}\v{B} \\ &= \v{\c{A}A} \end{aligned} \]
Evaluating \(\v{A'}\), we find
\[ \begin{aligned} \v{A'} &= \v{B}\v{A}\v{B} \\ &= e^{-\v{b}\frac{\phi}{2}}(a_0 + \v{a})e^{-\v{b}\frac{\phi}{2}} \\ &= a_0 e^{-\v{b}\phi} + e^{-\v{b}\frac{\phi}{2}} \v{a}e^{-\v{b}\frac{\phi}{2}} \end{aligned} \]
which is, in fact...
The Lorentz Transformation
A vector in the same direction as the rotation
If we first look at the case where the vector being rotated is in the same direction as the rotation itself, ie. \(\v{a}\v{b} = \v{b}\v{a} = |\v{a}|\) and since \(\v{b}^2 = 1\), then \(\v{a} = |\v{a}|\v{b}\), we can further simplify the rotation:
\(
\begin{aligned}
\v{A'}
&= a_0 e^{-\v{b}\phi} + e^{-\v{b}\frac{\phi}{2}} \v{a}e^{-\v{b}\frac{\phi}{2}} \\
&= a_0 e^{-\v{b}\phi} + \v{a}e^{-\v{b}\phi} \\
&= a_0 (\cosh{\phi} - \v{b} \sinh{\phi}) + \v{a}(\cosh{\phi} - \v{b} \sinh{\phi}) \\
&= (a_0 \cosh{\phi} - \v{ab}\sinh{\phi}) + (\v{a}\cosh{\phi} - a_0 \v{b} \sinh{\phi}) \\
&= (a_0 \cosh{\phi} - |\v{a}|\sinh{\phi}) + \v{b}(|\v{a}|\cosh{\phi} - a_0 \sinh{\phi}) \\
&= \cosh{\phi}(a_0 - |\v{a}|\tanh{\phi}) + \v{b}\cosh{\phi}(|\v{a}| - a_0 \tanh{\phi}) \\
\end{aligned}
\)
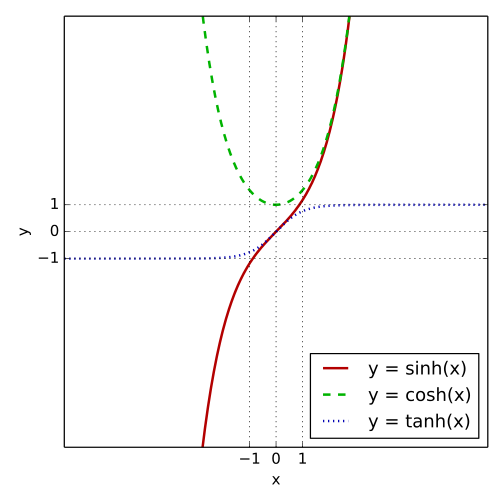
Plotting sinh, cosh and tanh
Note that \(\tanh\phi\) has the property of ranging from -1 to 1 (see figure) and that \(\cosh\phi\) and \(\tanh\phi\) can be related by:
\[ \cosh\phi = \frac{1}{\sqrt{1-\tan^2\phi}} \]
So with the substitution of \(v = \tanh\phi\), we're left with the Lorentz transformation of \(\v{A} = a_0 + \v{a}\):
\[ \v{B}\v{A}\v{B} = \frac{1}{\sqrt{1-v^2}}(a_0 - |\v{a}|v) + \frac{1}{\sqrt{1-v^2}}(|\v{a}| - a_0 v)\v{x} \]
A vector perpendicular to the direction of the rotation
Next let us look at the case where the vector being rotated is perpendicular to the rotation, ie. \(\v{a}\v{b} = -\v{b}\v{a}\). In this case:
\[ \begin{aligned} \v{A'} &= a_0 e^{-\v{b}\phi} + e^{-\v{b}\frac{\phi}{2}} \v{a}e^{-\v{b}\frac{\phi}{2}} \\ &= a_0 e^{-\v{b}\phi} + \v{a}e^{+\v{b}\frac{\phi}{2}} e^{-\v{b}\frac{\phi}{2}} \\ &= a_0 e^{-\v{b}\phi} + \v{a} \\ \end{aligned} \]
So the vector perpendicular to the direction of the rotation is not affected by the transformation, just as with the Lorentz transformation.